An extremely useful yet often forgotten strategy is listing things out. So many students overlook this strategy, dismissing it as non-mathematical, brute force, or inelegant, but as we'll see, some questions can ONLY be done by listing things out to reveal patterns.
To see how this works, here are three example SAT questions:
A) 25
B) 34
C) 42
D) 52
Instead of dilly-dallying, let's start by drawing a couple cases out, something you should do even if you don't know where it'll take you:
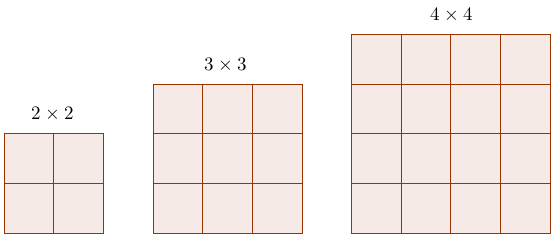
Now with each case, we'll just count the number of squares along the boundary to get \(k\).
For the \(2 \times 2\), we have \(k = 4\).
For the \(3 \times 3\), we have \(k = 8\).
For the \(4 \times 4\), we have \(k = 12\).
Do you notice a pattern for \(k\)?
You should've noticed that they're all multiples of 4. So the answer must be a multiple of 4.
The only multiple of 4 in the answer choices is D, 52.
We'll use the same tactic, starting with the smallest case.
The smallest tri-factorable number is simply \(1 \times 2 \times 3=\) 6.
Now 6 may seem like a long way from 1,000 but let's not give up just yet!
The next one up is \(2 \times 3\times 4=\) 24. If you keep going, you should get this list:
\(1 \times 2 \times 3= 6\)
\(2 \times 3 \times 4= 24\)
\(3 \times 4 \times 5= 60\)
\(4 \times 5 \times 6= 120\)
\(5 \times 6 \times 7= 210\)
\(6 \times 7 \times 8= 336\)
\(7 \times 8 \times 9= 504\)
\(8 \times 9 \times 10= 720\)
\(9 \times 10 \times 11= 990\)
Look how quickly we got there! Good things can happen if you just keep going.
If you count them up, you should see that the answer is 9.
Some of you might complain, "Ok it happened to work for this one question. What do you do when the list keeps on going and going?"
When that happens, making a list will still help, but another step or tactic will often be necessary.
Here's one example:
Again, let's start by listing some of them out:
\[102,\, 105,\, 108,\, 111,\, \ldots\]At this point, it's not hard to see that this will take forever. Here's the trick—instead of listing out all the numbers in the middle, let's list out a few at the end:
\[102,\, 105,\, 108,\, 111,\, \ldots 492,\, 495,\, 498\]Now let's divide each number in the list by 3:
\[34,\, 35,\, 36,\, 37,\, \ldots 164,\, 165,\, 166\]See what happened? The numbers are now consecutive. Now the question becomes, "How many numbers are there from 34 to 166?"
If you're not sure, ask yourself how many numbers there are from 5 to 10.
There are 6.
Now how did you get that?
Perhaps you didn't realize it, but you subtracted 5 from 10 and then added 1:
\[10 - 5 + 1 = 6\]So to get the number of numbers from 34 to 166, we do the same thing:
\[166 - 34 + 1 = 133\]Finally, we have the answer, 133.
Although this problem may seem long and complicated, the method we used to solve it applies to many other questions like this (namely, multiple questions). Once you understand it, solving similar questions is a breeze.
Hopefully, you now have a good grasp of how this works. Whenever you get stuck, it's good to have this strategy in mind. It's likely to be useful in questions dealing with:
- Multiples
- Questions with Different Cases or Possibilities
- How Many Questions
The more you practice, the better you'll get at spotting when this strategy should be used. So with that, I leave you with several practice questions that require this technique.
Practice Questions
- How many integers from 200 to 1000 are multiples of 6?
- In the integer 3,589 the digits are all different and increase from left to right. How many integers between 4,000 and 5,000 have digits that are all different and that increase from left to right?
- How many positive integers less than 1,000 are not divisible by 3?
- The sum of the positive odd integers less than 50 is subtracted from the sum of the positive even integers less than or equal to 50. What is the resulting difference?
A) 0
B) 25
C) 50
D) 100
Answers
- 133
- 10
- 666
- B
