
Just because the SAT has been revised doesn't mean there aren't any more tricky questions. In fact, there are just as many!
And the best way to conquer tricky questions is to do tricky questions. All of these questions are based on official SAT math questions.
Good luck!
Tricky SAT Math Questions
A calculator is permitted on all of the following questions.
- The football team has jerseys numbered from 10 to 30. Everyone gets a jersey and there are three leftover. How many people are on the football team?
- Derek is the 11th tallest person in the room and the 9th shortest. How many people are in the room?
- It takes 12 minutes to saw a log into four pieces. Given that each cut takes an equal amount of time, how many minutes would it take to saw the log into 6 pieces instead?
- In a tennis tournament, there are 100 players. Each match is played between two players. The winner advances and the loser is eliminated. Assuming a minimum number of byes (games in which a player automatically advanced due to no opponent), how many matches need to be played to determine a winner?
- At Groton High, Valentine’s Day is taken very seriously. Students in each class must send a valentine to all the other classmates. In a particular class, there are 72 valentines in total. How many students are in the class?
- A 50-foot ladder has rungs spaced 1 foot apart, starting 1 foot from each end. How many rungs are on the ladder?
- A straight fence is 150 feet long. Fenceposts are spaced 5 feet apart, with one post at each end of the fence. How many posts are there?
The length of a rectangle is increased by 50% and the width is decreased by 50%. How does the area of the rectangle change?
A) Decreases by 12.5%
B) Decreases by 25%
C) Increases by 25%
D) Stays the same-
John is a member of a gym that allows its members to get a free coaching session every 45 days. John receives his first coaching session on July 14th, which is the 195th day of the year. Which of the following inequalities can be used to determine the number of coaching sessions, \(n\), that John may receive this year? (Assume 1 year = 365 days.)
A) \(45n + 195 \leq 365\)
B) \(45(n - 1) + 195 \leq 365\)
C) \(45n - 1 + 195 \leq 365\)
D) \(45(n + 195) \leq 365\) -
A lightbulb manufacturer selects 500 incandescent bulbs from its factory at random and finds that their average lamp life has a 95% confidence interval of 1,000 to 2,000 hours. Which of the following conclusions is the most appropriate based on the confidence interval?
A) 95% of all the manufacturer's incandescent bulbs have a lamp life between 1,000 and 2,000 hours.
B) There is a 95% chance that an incandescent bulb made by the manufacturer has a lamp life between 1,000 and 2,000 hours.
C) The average lamp life of all the manufacturer's incandescent bulbs is likely between 1,000 and 2,000 hours.
D) There is a 95% chance that the average lamp life of all the manufacturer's incandescent bulbs is between 1,000 and 2,000 hours. -
The number of trees in a forest decreased by 25% from 2005 to 2006. If there were \(n\) trees in the forest in 2006, how many trees were there in 2005, in terms of \(n\)?
A) \(\dfrac{6}{5}n\)
B) \(\dfrac{5}{4}n\)
C) \(\dfrac{4}{3}n\)
D) \(\dfrac{3}{2}n\) -
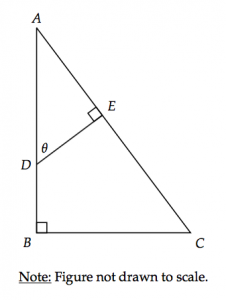
In the figure above, \(DE = 12\) and \(AC = 30\). If \(\sin\theta \approx 0.643\) and \(\cos\theta \approx 0.766\), what is the approximate length of \(\overline{AB}\)?
A) 18.43
B) 19.29
C) 22.98
D) 23.56
I'm not going to post answers or explanations for now because I'm cruel and I'd like you to think them through in the comments. But if you really need them, feel free to message me through the contact form.
