1. Triangle Inequality Theorem
Example: In \(\triangle ABC\), \(AB\) has a length of \(3\) and \(BC\) has a length of \(4\). How many integer values are possible for the length of \(AC\)?
Solution: The golden rule of any geometry problem is to draw a picture:
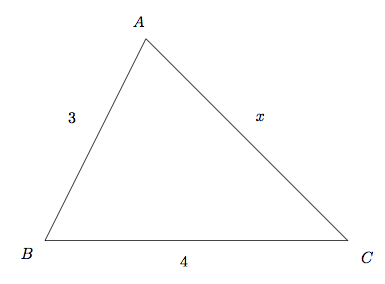
Based on the theorem, we can come up with
\[3 + 4 \gt x\] \[3 + x \gt 4\] \[4 + x \gt 3\]Which simplifies to
\[7 \gt x\] \[x \gt 1\] \[x \gt -1\]From these inequalities, only the first two matter since the third is always taken care of by the first two. Therefore, \(1 \lt x \lt 7\), and there are 5 integer values of \(x\).
2. Absolute Value
Example: A manufacturer of cookies tests the weight of its cookie packages to ensure consistency in the product. A package of cookies must weigh between \(16\) ounces and \(18\) ounces as it comes out of production. If \(w\) is the weight of an accepted cookie package, then which of the following inequalities correctly expresses all possible values for \(w\)?
A) \(\left|w + 17\right| \lt 1\)
B) \(\left|w - 17\right| \gt 1\)
C) \(\left|w + 17\right| \gt 1\)
D) \(\left|w - 17\right| \lt 1\)
Solution: Notice that \(16 \lt w \lt 18\). That means \(w\) must be within \(1\) ounce of \(17\). Hence, the answer is D. Notice that \(\left|w - 17\right|\) is how far off the weight is from \(17\) ("margin of error"), and this margin of error must be less than \(1\).
3. Area of an Equilateral Triangle
Example: What is the area of an equilateral triangle of side length \(4\)?
A) \(2\)
B) \(2\sqrt{3}\)
C) \(4\)
D) \(4\sqrt{3}\)
Solution: Using the formula (which can easily be derived by using \(30-60-90\) triangles), we get
\[\text{Area} = \dfrac{\sqrt{3}}{4}(4)^2 = 4\sqrt{3}\]The answer is D.
4. Semiannual Compound Interest
Example: Frank deposits $1,000 into a bank account that earns 5% interest compounded semianually. Which of the following is closest to the total amount in the account after 6 years?
A) $1,160
B) $1,340
C) $1,345
D) $1,796
Solution: Interest is earned \(6\times 2 = 12\) times.
\[\text{Total Amount} = \$1,000(1.025)^{12} \approx \$1,345\]The answer is C.
5. Inequalities
Example:
\[-15n \leq -5(n - 4)\]Which of the following represents the solutions to the inequality shown above?
A) \(n \leq -2\)
B) \(n \geq -2\)
C) \(n \leq 2\)
D) \(n \geq 2\)
Solution:
\[-15n \leq -5(n - 4)\] \[-15n \leq -5n + 20\] \[-10n \leq 20\]To isolate \(n\), we now have to divide both sides by \(-10\). Because we're dividing by a negative number, we have to reverse the sign.
\[n \geq -2\]The answer is B.
6. Direct and Indirect Proportion
Indirect proportion: \(xy = k\) or \(y = \dfrac{k}{x}\), where \(k\) is a constant
Example: A stone falls from a cliff. The distance it falls is directly proportional to the square of the time it has been falling. The stone falls \(19.6\) meters after \(2\) seconds. How far does it fall after \(3\) seconds?
Solution: Let's use the direct proportion equation:
\[d = kt^2\]It's important that we use \(t^2\) instead of \(t\) because as the problem specifies, the distance if proportional to the square of the time.
Now let's solve for \(k\):
\[19.6 = k \cdot (2)^2 \] \[19.6 = 4k\] \[k = 4.9\]So now our equation becomes
\[ d = 4.9t^2\]And when \(t = 3\),
\[d = 4.9\cdot (3)^2\] \[d = \boxed{44.1}\]7. Radius drawn to a Tangent
Example:
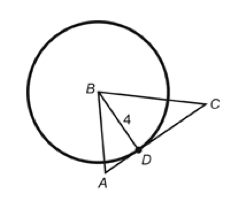
In the figure above, the center of the circle is point \(B\), and \(\overline{AC}\) is tangent to the circle at point \(D\). If \(AD = 2\) and \(DC = 5\), how much greater is the area of \(\triangle DBC\) than the area of \(\triangle ABD\)?
A) \(2\)
B) \(5\)
C) \(6\)
D) \(\text{It cannot be determined from the information given.}\)
Solution: Given the above rule, both \(\angle BDA\) and \(\angle BDC\) are right angles, making it easy to find the areas of the two triangles:
\[\text{Area of } \triangle DBC = \dfrac{5\cdot 4}{2} = 10\] \[\text{Area of } \triangle ABD = \dfrac{2\cdot 4}{2} = 4\]So the difference between the two areas is 6, answer C.
Your Turn: Practice Questions
For how many different integers \(x\), with \(2 \lt x \lt 7\), is there a triangle with sides of length \(2, 7,\) and \(x\)?
A) One
B) Two
C) Three
D) FourRolls of tapes must be made to a certain length. They must contain enough tape to cover between \(400\) feet and \(410\) feet. If \(l\) is the length of a roll of tape that meets the requirement, which of the following inequalities expresses the possible values for \(l\)?
A) \(\left|l - 400\right| \lt 10\)
B) \(\left|l - 405\right| \gt 5\)
C) \(\left|l + 405\right| \lt 5\)
D) \(\left|l - 405\right| \lt 5\)-
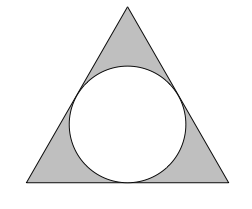
In the figure shown above, a circle is inscribed inside an equilateral triangle with a side length of \(6\). What is the area of the shaded region? (Hint: You'll need to use the \(30-60-90\) triangle relationship.)
A) \(6\sqrt{3} - 3\pi\)
B) \(6\sqrt{3} - 6\pi\)
C) \(9\sqrt{3} - 3\pi\)
D) \(9\sqrt{3} - 6\pi\) Melanie leaves $500 in a bank account that earns 8% interest compounded annually for 10 years. To the nearest dollar, how much more money would she have earned over the 10 year period if the interest had been compounded semiannually instead of annually?
A) 16
B) 18
C) 20
D) 25- If \(2m - 3 \geq 17\) and \(-3n + 5 \geq -7\), what is the minimum possible value of \(m - n\)?
\(y\) is inversely proportional to \(x\) and \(y = 8\) when \(x = 3\). What is the value of \(y\) when \(x = 4\)?
A) \(5\)
B) \(6\)
C) \(7\)
D) \(8\)-
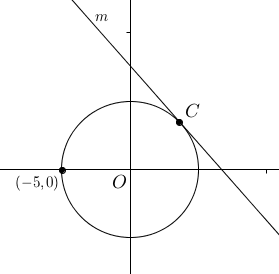
The coordinates \((x, y)\) of each point on the circle above satisfy the equation \(x^2 + y^2 = 25\). Line \(l\) is tangent to the circle at point \(C\). If the \(x\)-coordinate of point \(C\) is \(3\), what is the slope of \(l?\)
Answers:
- A
- D
- C
- A
- 6
- B
- \(-\dfrac{3}{4}\)
