12 Classic SAT Math Questions You Must Know How to Solve

Most tests you take in your average math class are straightforward and obvious. As long as you’ve studied the concepts, you know what to do when you encounter a problem. You know what to expect.

On the SAT, however, even great math students may not know where to begin. Even if you know all the concepts, you won’t always know which ones to apply and how. To answer the tough questions, you need a combination of experience and a willingness to try things out.

I always warn new students that the SAT Math is unlike most tests they’ve done in school. But when they ask how it’s different, I usually have to resort to vague terms like "problem-solving, creative thinking, and word questions."

So here are 12 SAT questions that illustrate frequently tested ideas and ways of thinking that go beyond standard school material. I’ve included questions across all test topics—from algebra to geometry to logic.

All of them are tough! Try them on your own. Hints are available at the bottom and answers will be available in another post.

The Questions

  1. If \(2^x + 2^x + 2^x + 2^x = 2^{16}\), what is the value of \(x\)?
  2. The lengths of two sides of a triangle are \(4\) and \(9\). What is the greatest possible integer length of the third side?
  3. A car traveled \(10\) miles at an average speed of \(30\) miles per hour and then traveled the next \(10\) miles at an average speed of \(50\) miles per hour. What was the average speed, in miles per hour, of the car for the \(20\) miles?
  4. The average (arithmetic mean) age of a group of \(15\) teachers is \(40\) years. If \(6\) additional teachers are added to the group, then the average age of the \(21\) teachers is \(44\) years. What is the average age of the \(6\) additional teachers?
  5. Let the function \(f\) be defined by \(f(x) = x^2 + 18\). If \(a\) is a positive number such that \(f(2a) = 3f(a)\), what is the value of \(a\)?
  6. A tech company bought a number of computers for its employees: \(6\) costing \(\$1600\) each, \(4\) costing \(\$1200\) each, and \(y\) costing \(\$900\) each, where \(y\) is a positive odd integer. If the median price for all the computers purchased by the company was \(\$1200,\) what is the greatest possible value of \(y\)?
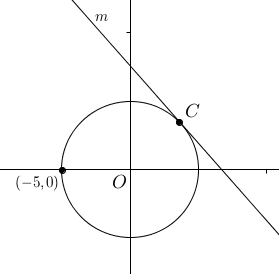  7. SAT Circle QuestionThe coordinates \((x, y)\) of each point on the circle above satisfy the equation \(x^2 + y^2 = 25\). Line \(m\) is tangent to the circle at point \(C\). If the \(x\)-coordinate of point \(C\) is \(3\), what is the slope of \(m?\)
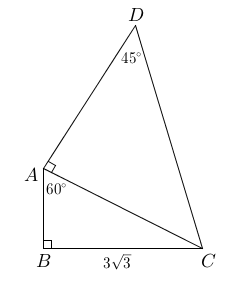  8. SAT Triangle QuestionWhat is the length of \(CD\) in the figure above?
    A) \(4\)
    B) \(4\sqrt{2}\)
    C) \(6\)
    D) \(6\sqrt{2}\)
  9. If \(0\leq a \leq b\) and \((a + b)^2 - (a-b)^2 \geq 9\), what is the least possible value of \(b\)?
  10. In triangle \(ABC\), the measure of angle \(A\) is equal to \(2x^\circ + 20^\circ\) and the measure of angle \(B\) is equal to \(x^\circ + 46^\circ\). If \(\sin\angle A = \cos\angle B\), what is the value of \(x\)?
  11. \[f(t) = 800(1,000)^{\frac{t}{27}}\] The function \(f\) above represents the current total population of sand sharks off the coast of Greenland \(t\) years after 1980. To the nearest year, how many years did (or will) it take for the population to be 10 times larger than it was in 1980?
  12. In order to fulfill a prescription for 200 milliliters (mL) of a medication at a 55% solution, a pharmacist must mix \(x\) mL of a 40% solution with \(y\) mL of a 60% solution. What is the value of \(x\)?

Hints

  1. The answer is NOT 4. You can only add exponents when the terms are being multiplied. Think about how many \(2^{x}\)s there are.
  2. The answer is NOT "as big as you want." Look up the Triangle Inequality Theorem.
  3. The answer is NOT 40. This is much harder than that. Remember that
    distance \(=\) rate \(\times\) time
  4. Think about the sums of all the ages.
  5. No hint for this one. If you truly understand functions, you'll get this.
  6. No hint for this one either.
  7. What is the slope of \(\overline{OC}\)?
  8. Know your special triangles (30-60-90 and 45-45-90).
  9. First, expand (FOIL) and simply. Now how do the values of \(a\) and \(b\) affect each other when they are increased or decreased?
  10. You'll have to use a certain trigonometric identity.
  11. Use the fact that \(1,000 = 10^3\)
  12. 200 milliliters of a 55% solution contains how many milliliters of the actual medication?

Answers

I'm not going to post answer explanations (at least for now), because I want you to figure these out on your own. What I will do is post the answers, so you can check/review your work.

  1. \(14\)
  2. \(12\)
  3. \(\frac{75}{2}\) or \(37.5\)
  4. \(54\)
  5. \(6\)
  6. \(9\)
  7. \(-\frac{3}{4}\)
  8. \(D\)
  9. \(\frac{3}{2}\) or \(1.5\)
  10. \(8\)
  11. \(9\)
  12. \(50\)