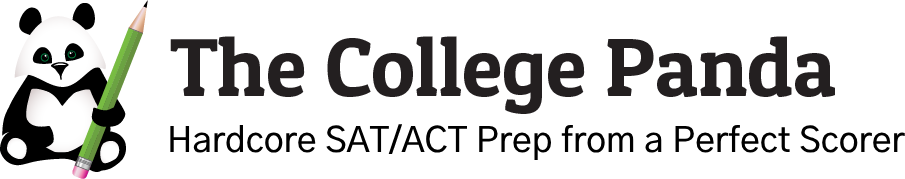The SAT will sometimes throw in a question on function transformations. This question can range from easy to difficult, so it's important to understand the entire concept. For example, take a look at the following official example taken from The College Board's Question of the Day app:
Example Function Tranformation SAT Question
The graph of the function \(f\) is the graph of the function \(g\) compressed horizontally by a factor of 2 and reflected over the \(y\)-axis. Which of the following correctly defines the function \(f\)?
A) \(f(x) = g(-2x)\)B) \(f(x) = -g(2x)\)
C) \(f(x) = 2g(-x)\)
D) \(f(x) = -2g(x)\)
Before we get to the solution, let's review the transformations you need to know using our own example function
\[f(x) = x^2 + 2x\]whose graph looks like
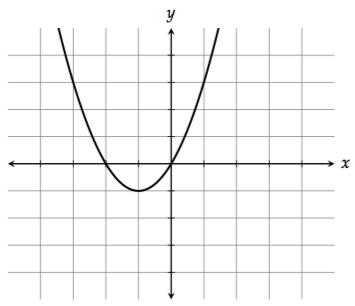
1. Shifting up and down
To shift the graph up, add a constant at the end of the function. For example, \(f(x) + 2 = x^2 + 2x + 2\) would shift the graph up 2 units.
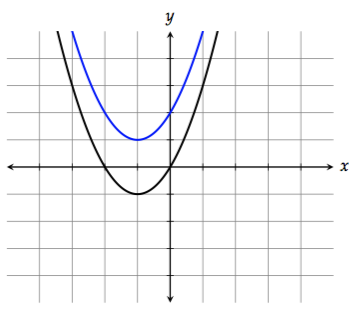
To shift the graph down, subtract a constant at the end of the function. \(f(x) - 2 = x^2 + 2x - 2\) would shift the graph down 2 units.
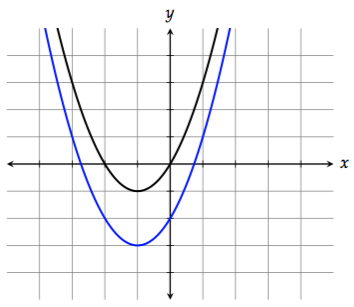
2. Shifting left and right
To shift the graph to the left by 1 unit, replace \(x\) with \(x + 1\):
\[f(x + 1) = (x + 1)^2 + 2(x + 1)\]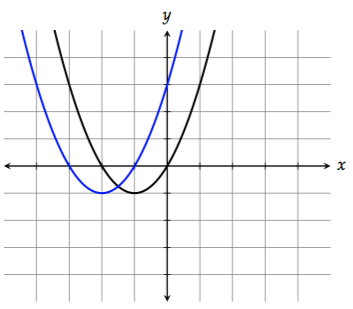
To shift the graph to the right by 1 unit, replace \(x\) with \(x - 1\):
\[f(x - 1) = (x - 1)^2 + 2(x - 1)\]The substitutions for left and right are counterintuitive to a lot of students because they're the opposite of what you might expect.
3. Reflecting across the \(x\)-axis
To reflect the graph across the \(x\)-axis (flip it upside down), multiply the function by \(-1\):
\[-f(x) = -x^2 - 2x\]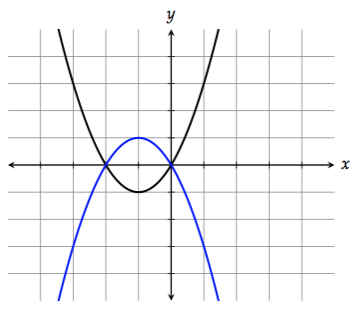
4. Reflecting across the \(y\)-axis
To reflect the graph across the \(y\)-axis, replace \(x\) with \(-x\):
\[f(-x) = (-x)^2 + 2(-x) = x^2 - 2x\]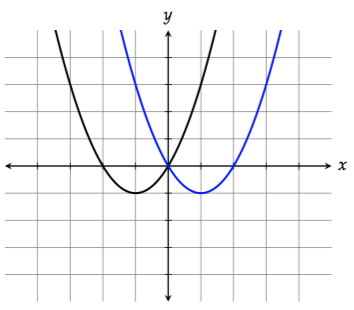
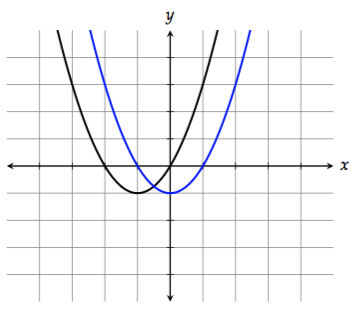
5. Stretching/Compressing vertically
To stretch the graph vertically by a factor of 2, multiply \(f(x)\) by 2:
\[2f(x) = 2(x^2 + 2x) = 2x^2 + 4x\]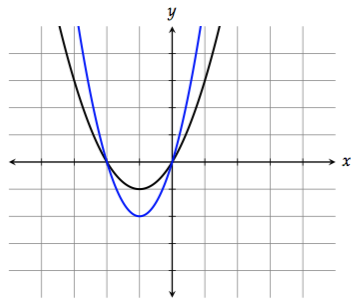
You can think of this as the graph getting "taller."
To compress the graph vertically by a factor of 2, multiply \(f(x)\) by \(\dfrac{1}{2}\):
\[\dfrac{1}{2}f(x) = \dfrac{1}{2}(x^2 + 2x) = \dfrac{1}{2}x^2 + x\]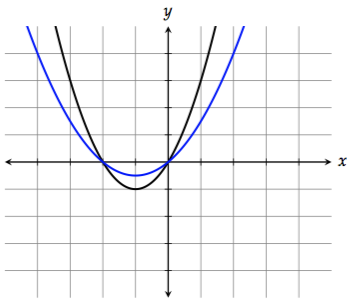
Think of this as the graph getting "shorter."
6. Stretching/Compressing horizontally
To stretch the graph horizontally by a factor of 2, replace \(x\) with \(\dfrac{1}{2}x\):
\[f\left(\dfrac{1}{2}x\right) = \left(\dfrac{1}{2}x\right)^2 + 2\left(\dfrac{1}{2}x\right) = \dfrac{1}{4}x^2 + x\]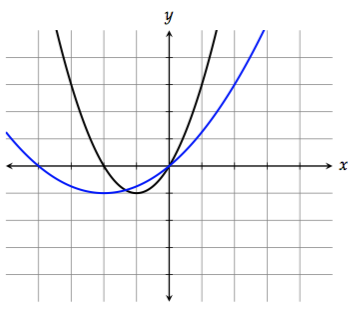
Notice that the right side doesn't get stretched as much. That's because the points on the right side of the graph have smaller \(x\)-values (absolute value-wise). Doubling a small number doesn't do as much as doubling a large number.
To compress the graph horizontally by a factor of 2, replace \(x\) with \(2x\):
\[f(2x) = (2x)^2 + 2(2x) = 4x^2 + 4x\]By the way, these substitutions for horizontal stretch and compression are also counterintuitive to a lot of students. Be careful of horizontal transformations (shifting left and right, stretching/compressing). It's often the opposite of what you might expect.
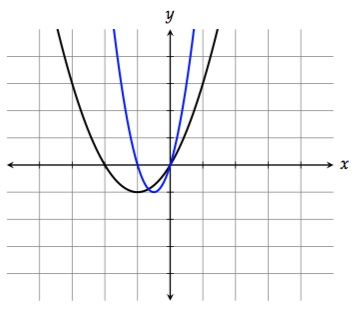
Notice that the right side doesn't get compressed as much. That's because the points on the right side of the graph have smaller \(x\)-values (absolute value-wise). Halving a small number doesn't do as much as halving a large number.
7. Absolute Value
To reflect all the points on the graph with negative \(y\)-values across the \(x\)-axis, take the absolute value of the function:
\[\left|f(x)\right| = \left|x^2 + 2x\right|\]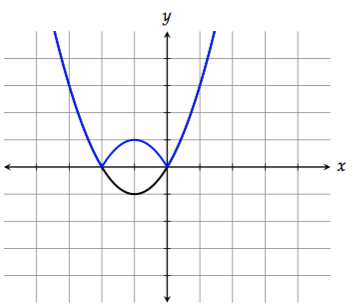
Back to the Example
Getting back to the example question at the beginning of this post, we want to compress \(g\) horizontally by a factor of 2 and reflect it over the \(y\)-axis. Given what we've learned, this is pretty easy.
To compress the graph horizontally by a factor of 2, we replace \(x\) with \(2x\):
\[g(2x)\]To reflect the graph over the \(y\)-axis, we replace \(x\) with \(-x\):
\[g(2(-x)) = g(-2x)\]The answer is A.